Jordan Ellenberg tells us how to use mathematical thinking to “not be wrong”. He tells us about mathematical thinking, cons, and finding results.
Good Advice
The advice is often very good. If he wants to call it as a result of mathematics that works for me. Following his advice will help us have better judgment. You will also avoid a few cons. He explains the “Baltimore Stockbroker” con. This is an inventive con which works because “improbably things happen a lot” (Ellenberg, 2014, page 99). That might sound a bit odd but it makes sense. If you do things enough times improbable things will happen, “what is improbable is probable” (Ellenberg, 2014, page 99).
The Baltimore Stockbroker Con
The Baltimore stockbroker sends out predictions to a large number of people over multiple weeks. By the end you might see lots of correct predictions. You, therefore, think the stockbroker has a magic secret. He doesn’t.
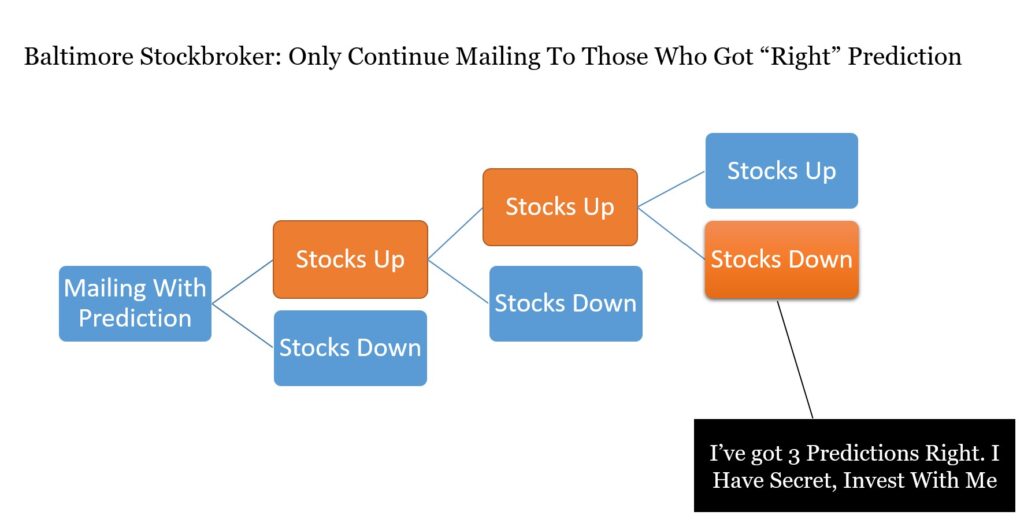
The secret is simple. Lots of mailings were sent with different predictions. Only those who got a correct first prediction got a second mailing. This mailing was again different to different people. Only those who got a correct second prediction got a third etc… Eventually, a small number of people have received a string of correct predictions. The successful prediction looks unlikely to have occured by chance. Yet, this is only because those getting the correct predictions don’t know that a huge number of people got failed predictions. You don’t see how much wiggle room the stockbroker has got. The con works if the financial return from those convinced is more than the postage for the vast amount of failed predictions.
Random Noise Looks Like A Pattern From The Right Angle
Such wiggle room means you typically will find results if you look enough. Random noise will look like a pattern. Ellenberg describes the academic community as “running the con on themselves” (Ellenberg, 2014, page 152). When we run lots of experiments and ditch the failures in a “file drawer” we can end up believing that random results actually mean something.
The downside of a failure to notice the implications of math is shown by the story of Harold Hotelling responding to research showing the “Triumph of Mediocrity”. This research purported to show that competition forced mediocrity on business. Hotelling noted this was just regression to the mean. Those who are picked when they are doing well are typically being lucky (as well as good). Luck runs out and they tend to look more normal, e.g., mediocre, over time. I do feel sorry for the guy who had spent years researching only to be shown that he had just illustrated an already well-known mathematical finding. Knowing a bit of math might help one not be wrong.
For more on math see here and regression to the mean see here.
Read: Jordan Ellenberg (2014) How not to be wrong: the power of mathematical thinking, Penguin Books
