While statistics can help us understand the world there is plenty of opportunity to abuse them to mislead. Darrell Huff wrote a short book that was first published in 1952 on lying with statistics. Some of the text shows its age (lots of male pronouns and references to gentleman) but many of the lessons remain applicable today. Reading Huff’s advice and teach yourself how not to be lied to with statistics.
Lying With Statistics: The Biased Sample
Huff works through a number of problems in the way statistics are presented. First he notes the problem of bias in the sample used. This is a classic challenge of survey research: you must ensure those you ask are representative of whoever you are studying.
Lying With Statistics: The Mean Of A Varied Group
He highlights the problem of using the mean when there is a large variance of outcomes. The mean of nine people with no income and someone gaining ten million dollars a year is $1 million. This seems misleading as most people aren’t doing well. An alternative measure of the average, the median or middle value, shows the average person earning nothing.
Lying With Statistics: Small Samples And Statistical Ties
Conclusions being drawn from too small samples is something that annoys Huff. Huff also doesn’t like it when conclusions are drawn despite results being statistically tied. This happens all the time in the reporting of election polling. One candidate appears to be ahead with 51% versus the other candidate’s 49% but the result is within the margin of error. They are essentially the same.
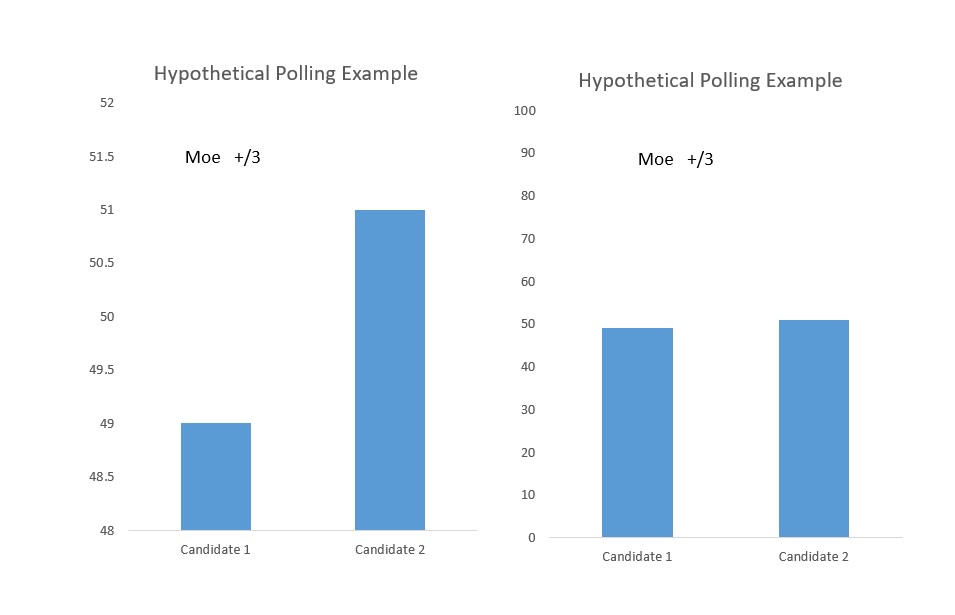
Lying With Statistics: Graphs
His thoughts on graphs seem painfully relevant today. I’ve seen plenty of graphs without numbers on the Y-axis (or even numbers on the X-axis sometimes). Such graphs are worse than useless. When I see them I hope these graphs are meant to mislead. The alternative seems to be that the presenter doesn’t know what they are doing.
Lying With Statistics: Context And Academic Bias
He complains about context being removed and also that people conclude that something that comes after something else must have been caused by the earlier event.
Huff notes that: “Even the man in academic work may have a bias (possibly unconscious) to favor, a point to prove, an axe to grind” (Huff, 1993, page 123). That anyone could say such a thing is shocking to me. Still academics should bear this in mind. Lets try and make sure that we don’t, and that our colleagues don’t, mislead with statistics. At the very least we should always label our Y-axis.
Read: (1993) How To Lie with Statistics, WW Norton, 1st Revised Edition
For more one visualization see here.
